Koordinatenformate
Das System, in dem Koordinatenangaben auf der Erde in Form zweier Zahlen (Längengrad und Breitengrad) angegeben sind, ist schon alt und beruht auf der idealisierten Annahme, dass die Erde eine ideale Kugel ist. Dadurch ergibt sich nachstehendes Bild.
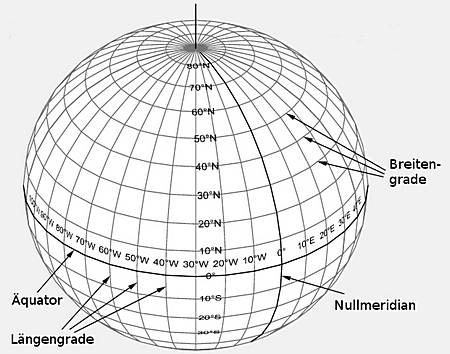 Die Breitengrade sind dabei quer und parallel zueinander verlaufende Schnitte durch die Erde, die die Erde dabei bildlich in Scheiben zerlegen, mit parallel verlaufenden Schnittebenen, aber mit unterschiedlicher Scheibendicke - im Bild in Scheiben zu je 10 Grad. Die dickste Stelle, genau in der Mitte, ist der Äquator. Er zerlegt die Erde in eine Nord- und eine Südhalbkugel. Nach Norden und nach Süden hin werden die Scheiben ab hier immer kleiner (sowohl Durchmesser als auch Scheibendicke). Die Breitengrade zählt man vom Äquator ausgehend nach oben von 0° am Äquator bis 90° Nord am Nordpol, nach unten Richtung Süden geht die Zählung von 0° bis 90° Süd, oder kurz: -90° am Südpol. Positive Breitengrade bezeichnen also immer Angaben nördlich, negative hingegen südlich des Äquators.
Die Breitengrade sind dabei quer und parallel zueinander verlaufende Schnitte durch die Erde, die die Erde dabei bildlich in Scheiben zerlegen, mit parallel verlaufenden Schnittebenen, aber mit unterschiedlicher Scheibendicke - im Bild in Scheiben zu je 10 Grad. Die dickste Stelle, genau in der Mitte, ist der Äquator. Er zerlegt die Erde in eine Nord- und eine Südhalbkugel. Nach Norden und nach Süden hin werden die Scheiben ab hier immer kleiner (sowohl Durchmesser als auch Scheibendicke). Die Breitengrade zählt man vom Äquator ausgehend nach oben von 0° am Äquator bis 90° Nord am Nordpol, nach unten Richtung Süden geht die Zählung von 0° bis 90° Süd, oder kurz: -90° am Südpol. Positive Breitengrade bezeichnen also immer Angaben nördlich, negative hingegen südlich des Äquators.
Die Breitengrade haben, wenn man sich auf der Erdoberfläche exakt in Richtung Norden oder Süden bewegt, überall den gleichen Abstand voneinander. Das heißt, von 0° am Äquator zu 1° Nord ist es genauso weit wie von 45° Nord zu 46° Nord oder von 89° Nord bis zum geographischen Nordpol, nämlich pro Grad genau 60 Seemeilen oder 111,18 Kilometer.
Eine Seemeile (1,853 km) war früher definiert als die Strecke, die ein Schiff auf dem Äquator nach Osten oder Westen fahren musste, damit es eine Bogenminute, also 1/60 Grad Strecke zurücklegt.
Die von Nord nach Süd verlaufenden Längengrade teilen die Erde nicht in gerade Scheiben. Sie treffen sich alle an zwei Punkten, nämlich am geographischen Nord- und am Südpol. Sie teilen damit die Erde etwa so wie wenn man Scheiben aus einer Melone schneidet. Würde man am Äquator einmal um die Erde laufen können, so würde man eine Strecke von ziemlich genau 40.000 Kilometern zurücklegen (60 x 360 = 21.600 Seemeilen). Bedingt durch die Kugelform laufen die Längengrade zu den Polen hin immer weiter zusammen. Geht man beispielsweise ganz im Süden Deutschlands (der liegt auf etwa dem 47. nördlichen Breitengrad) genau eine Längenminute (1/60 Längengrad) nach Osten oder Westen, so beträgt diese Strecke keine Seemeile (1,853 km) mehr, sondern nur noch 1,264 km. Derselbe Versuch im Norden Deutschlands, auf 55 Grad nördlicher Breite durchgeführt (da liegt die Nordspitze Sylts) bringt einen auf einer Längenminute nur noch 1,063 km voran und im Norden des schottischen Festlands (auf 58,5° Nord) sind es mit 968 Metern schon deutlich unter einem Kilometer.
Wichtig bei den Längengraden ist außerdem noch der sog. Nullmeridian, das ist der Längengrad, von dem aus die Zählung beginnt: nach Osten (=nach rechts) von 0° bis 180° Ost, nach Westen (nach links) von 0° bis 180° West oder bis -180°. Der Nullmeridian läuft übrigens durch den Londoner Stadtteil Greenwich und dort durch die historische Sternwarte Royal Greenwich Observatory. Er wird deshalb auch als Greenwich-Meridian bezeichnet. Sein Verlauf wurde willkürlich und wurde während einer Meridiankonferenz Ende des 19. Jahrhunderts so festgelegt.
Anzeigeformate / Schreibweisen
Jede Koordinatenangabe besteht also aus zwei Teilen: dem Breitengrad und dem Längengrad. Man spricht hier deshalb auch oft von einem Koordinatenpaar. Für die Anzeige hat sich eingebürgert, dass man der jeweiligen Gradangabe ein N oder S (Nord bzw. Süd) beim Breitengrad voranstellt und beim Längengrad ein W oder E (West oder East). Auch im deutschen Sprachraum hat sich E für Ost (East) etabliert, weil ein O schlicht und einfach zu leicht mit der Ziffer Null verwechselt werden könnte.
Außerdem existieren drei gebräuchliche Schreibweisen nebeneinander:
- Dezimalgrad, also eine Zahl mit Nachkommmastellen (typischerweise werden vier bis sechs Nachkommastellen angegeben)
- Ganze Grad und nachgestellte Bogenminuten, wobei die Minuten mit drei Nachommastellen angegeben werden
- Ganze Grad, ganze Bogenminuten und Bogensekunden, letztere mit maximal einer Nachkommastelle
Bogenminuten und Bogensekunden berechnen sich übrigens genauso wie Minuten und Sekunden bei der Uhrzeit. Ein Grad hat dabei 60 Bogenminuten und eine Bogenminute besteht aus 60 Bogensekunden. Die drei unterschiedlichen Schreibweisen kann man ineinander umrechnen, was ich anhand eines Beispiels erklären möchte.
Beispiel: In der irischen Hauptstadt Dublin steht das Museum "Guiness Storehouse", in dem man sich über die 250 Jahre alte Geschichte des Guinness-Bieres informieren kann. Es hat, in Dezimalgrad dargestellt, die Koordinaten: N53.34167° W6.28694°
Um in die oben genannte zweite Möglichkeit umzurechnen, also in Grad und Bogenminute mit 3 Nachkommastellen, muss man lediglich den Nachkommaanteil mit 60 multiplizieren. Bei N53.34167 also 0.34167 x 60 = 20.500 und damit wird die Breitenangabe zu N53° 20.500'. Genauso verfährt man mit der Längenangabe: 0.28694 x 60 = 17.2164 und auf drei Stellen gerundet ergibt sich W6° 17.216'. Die gesamte Ortsangabe des Museums in dieser Schreibweise lautet damit: N53° 20.500' W6° 17.216'
Bleibt nur noch die dritte Möglichkeit, nämlich die Darstellung in Grad, Bogenminute und Bogensekunde. Hierfür nimmt man nun die Nachkommastellen der Minuten mal 60 und erhält die Sekunden. Aus 20.500' werden so 20' und 30" und aus 17.216' werden 17' und 13". Die gesamte Ortsangabe ist dann: N53° 20' 30" W6° 17' 13"
Probieren Sie es aus: Rufen Sie GoogleMaps auf und geben Sie in dem Suchfeld eine der drei oben fett dargestellten Koordinatenangaben ein (am besten mit der Maus markieren, dann kopieren und im Suchfeld einfügen). Jede der drei Angaben wird Ihnen exakt denselben Punkt in GoogleMaps zeigen. Tatsächlich werden alle Angaben mit Ausnahme der ersten intern zunächst ins Dezimalformat umgerechnet, weil sich damit am einfachsten rechnen lässt.
UTM-Format
Um die sich nach oben "verjüngenden" Längengrade auszugleichen und ein System mit möglichst wenig Rechenaufwand verwenden zu können, wurde das UTM-Koordinatensystem eingeführt. Es ist ebenfalls global gültig, aber nur in den Breitengraden von 80° Süd bis 84° Nord. Mit UTM-Koordinaten lässt es sich wesentlich leichter rechnen als mit dem oben dargestellten, auf Breiten- und Längengraden basierenden Koordinatensystem. Die Umrechnung der Koordinaten ineinander ist aber ein wenig komplizierter. Das Tool auf der folgenden Seite nimmt die Umrechnung für Sie vor.
Prinzipiell wird beim UTM-Koordinatensystem die Erde (von ein paar Ausnahmen ganz im Norden und im Süden) in Längsstreifen zu je 6 Grad Ost-West-Ausdehnung aufgeteilt. Da die Längengrade von 180° West bis 180° Ost gehen, also 360 Längengrade umfassen, erhält man so genau 60 Streifen. Die Streifen werden UTM-Zonen genannt und sie sind einfach von 01 bis 60 durchnummeriert, beginnend bei 180° West bis 174° West mit der Zone 01, 174° W bis 168° W ist Zone 02 u.s.w. Deutschland liegt größtenteils in den UTM-Zonen 32 und 33, also zwischen 6° Ost und 18° Ost.
Von Süden nach Norden ist die Erde bei den UTM-Koordinaten außerdem in sogenannte Zonenfelder (jeweils acht Breitengrade umfassend) aufgeteilt, die mit einem einfachen Buchstaben bezeichet werden: von S80° bis S72° ist es der Buchstabe C, dann bis S64° Buchstabe D u.s.w. bis hoch zum Buchstaben X, welcher von N72° bis N84° reicht. Die Buchstaben I und O werden wegen Verwechslungsgefahr mit dem Buchstaben J und der Ziffer 0 nicht verwendet. Die Grenze zwischen Süd- und Nordhalbkugel wird durch die Zonenfelder M (von 8° Süd bis zum Äquator) und N (vom Äquator bis 8° Nord) bestimmt. Alles ab N aufwärts befindet sich also auf der Nordhalbkugel.
Die so entstehenden, kleineren (im Vergleich zur Erdoberfläche) Vierecke werden nun in die Ebene projiziert. Rein technisch können Sie sich das so vorstellen: Sie schneiden ein kleines Viereck aus der Schale einer Orange aus und drücken es flach auf eine Tischplatte. Die Krümmung geht dadurch verloren, auch wenn sich die Ränder des Vierecks dabei ein wenig verziehen.
Auf die so in die Ebene projizierten Vierecke kann man nun ein ebenes (kartesisches) Koordinatensystem legen, mit einer X- und einer Y-Achse. Die X-Achse geht dabei nach rechts, die Y-Achse nach oben. Entsprechend werden die beiden Angaben auch "Rechtswert" und "Hochwert" genannt, auf Englisch hat man sich die Himmelsrichtungen hier rein sprachlich bewahrt und spricht von "Easting" und "Northing".
Der Hochwert wird für die Nordhalbkugel von 0 an (auf dem Äquator) nach oben gezählt, und zwar pro zurückgelegtem Meter in Richtung Norden um 1. Geht man in Richtung Süden, so wird von 10.000.000 nach unten gezählt - einen Meter südlich des Äquators hat man also 9.999.999 als Hochwert. Die Angabe des Hochwerts ist damit maximal 7-stellig.
Für den Rechtswert ist das Vorgehen etwas anders. Hier wird für jedes Viereck ein Mittel-Meridian errechnet. Für die UTM-Zone 31 (von 0° bis 6° Ost) liegt er bei 3° Ost, für die Zone 32 (6° Ost bis 12° Ost) bei 9° Ost u.s.w., also immer in der Mitte. Auf dem Mittel-Meridian hat man immer einen Rechtswert von 500.000. Geht man nach links, so verringert sich dieser Wert um 1 pro Meter. Nach rechts erhöht er sich entsprechend. Die Rechtswerte springen damit an den UTM-Zonengrenzen. Beispiel: Der Längengrad E5,99999° hat einen Rechtswert von 714984 in der Zone 31, einen Schritt weiter östlich ist man auf E6,00000° und hat einen Rechtswert von nur noch 285016 - jetzt aber in der nächsten Zone 32.
UTM-Koordinaten werden immer mit allen vier Angaben geschrieben, und zwar in der Reihenfolge: Zone, Feld, Rechtswert, Hochwert. Beispiel: das Brandenburger Tor mit den Koordinaten N52° 30' 59" E13° 22' 40" hat die UTM- Koordinaten: 33 U 389923 5819712
Falls Sie sich für mehr Hintergründe und Einzelheiten des UTM-Koordinatensystems interessieren, empfehle ich Ihnen den Wikipedia-Artikel zu diesem Thema.